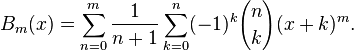Bernoulli Polynomials - Another Explicit Formula

Another Explicit Formula

An explicit formula for the Bernoulli polynomials is given by

B_m(x)= \sum_{n=0}^m \frac{1}{n+1} \sum_{k=0}^n (-1)^k {n \choose k} (x+k)^m.

Note the remarkable similarity to the globally convergent series expression for the Hurwitz zeta function. Indeed, one has

where ζ(s, q) is the Hurwitz zeta; thus, in a certain sense, the Hurwitz zeta generalizes the Bernoulli polynomials to non-integer values of n.

The inner sum may be understood to be the nth forward difference of xm; that is,

where Δ is the forward difference operator. Thus, one may write

This formula may be derived from an identity appearing above as follows. Since the forward difference operator Δ equals

where D is differentiation with respect to x, we have, from the Mercator series

As long as this operates on an mth-degree polynomial such as xm, one may let n go from 0 only up to m.

An integral representation for the Bernoulli polynomials is given by the Nörlund–Rice integral, which follows from the expression as a finite difference.

An explicit formula for the Euler polynomials is given by

E_m(x)= \sum_{n=0}^m \frac{1}{2^n} \sum_{k=0}^n (-1)^k {n \choose k} (x+k)^m\,.

This may also be written in terms of the Euler numbers Ek as

E_m(x)= \sum_{k=0}^m {m \choose k} \frac{E_k}{2^k} \left(x-\frac{1}{2}\right)^{m-k} \,.

Read more about this topic:  Bernoulli Polynomials

Famous quotes containing the words explicit and/or formula:

    “Like dreaming, reading performs the prodigious task of carrying us off to other worlds. But reading is not dreaming because books, unlike dreams, are subject to our will: they envelop us in alternative realities only because we give them explicit permission to do so. Books are the dreams we would most like to have, and, like dreams, they have the power to change consciousness, turning sadness to laughter and anxious introspection to the relaxed contemplation of some other time and place.”
    —Victor Null, South African educator, psychologist. Lost in a Book: The Psychology of Reading for Pleasure, introduction, Yale University Press (1988)

    “I cannot give you the formula for success, but I can give you the formula for failure—which is: Try to please everybody.”
    —Herbert B. Swope (1882–1958)