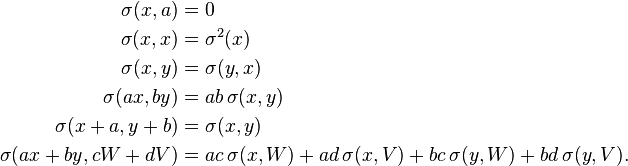Covariance - Properties

Properties

  • Variance is a special case of the covariance when the two variables are identical:
  • If x, y, W, and V are real-valued random variables and a, b, c, d are constant ("constant" in this context means non-random), then the following facts are a consequence of the definition of covariance:
\begin{align} \sigma(x, a) &= 0 \\ \sigma(x, x) &= \sigma^2(x) \\ \sigma(x, y) &= \sigma(y, x) \\ \sigma(ax, by) &= ab\, \sigma(x, y) \\ \sigma(x+a, y+b) &= \sigma(x, y) \\ \sigma(ax+by, cW+dV) &= ac\,\sigma(x,W)+ad\,\sigma(x,V)+bc\,\sigma(y,W)+bd\,\sigma(y,V). \end{align}

For sequences x1, ..., xn and y1, ..., ym of random variables, we have

For a sequence x1, ..., xn of random variables, and constants a1, ..., an, we have

Read more about this topic:  Covariance

Famous quotes containing the word properties:

    “A drop of water has the properties of the sea, but cannot exhibit a storm. There is beauty of a concert, as well as of a flute; strength of a host, as well as of a hero.”
    —Ralph Waldo Emerson (1803–1882)

    “The reason why men enter into society, is the preservation of their property; and the end why they choose and authorize a legislative, is, that there may be laws made, and rules set, as guards and fences to the properties of all the members of the society: to limit the power, and moderate the dominion, of every part and member of the society.”
    —John Locke (1632–1704)