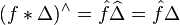Dirac Comb
A so-called uniform "pulse train" of Dirac delta measures, which is known as a Dirac comb, or as the Shah distribution, creates a sampling function, often used in digital signal processing (DSP) and discrete time signal analysis. The Dirac comb is given as the infinite sum, whose limit is understood in the distribution sense,
which is a sequence of point masses at each of the integers.
Up to an overall normalizing constant, the Dirac comb is equal to its own Fourier transform. This is significant because if ƒ is any Schwartz function, then the periodization of ƒ is given by the convolution
In particular,
is precisely the Poisson summation formula.
Read more about this topic: Dirac Delta Function
Famous quotes containing the word comb:
“Soldier, scholar, horseman, he,
As ‘twere all life’s epitome.
What made us dream that he could comb grey hair?”
—William Butler Yeats (1865–1939)