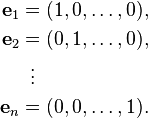Real Coordinate Space
Let R denote the field of real numbers. For any positive integer n, the set of all n-tuples of real numbers forms an n-dimensional vector space over R, which is denoted Rn and sometimes called real coordinate space. An element of Rn is written
where each xi is a real number. The vector space operations on Rn are defined by
The vector space Rn comes with a standard basis:
An arbitrary vector in Rn can then be written in the form
Rn is the prototypical example of a real n-dimensional vector space. In fact, every real n-dimensional vector space V is isomorphic to Rn. This isomorphism is not canonical, however. A choice of isomorphism is equivalent to a choice of basis for V (by looking at the image of the standard basis for Rn in V). The reason for working with arbitrary vector spaces instead of Rn is that it is often preferable to work in a coordinate-free manner (that is, without choosing a preferred basis).
Read more about this topic: Euclidean Space
Famous quotes containing the words real and/or space:
“Every age, every culture, every custom and tradition has its own character, its own weakness and its own strength, its beauties and cruelties; it accepts certain sufferings as matters of course, puts up patiently with certain evils. Human life is reduced to real suffering, to hell, only when two ages, two cultures and religions overlap.”
—Hermann Hesse (1877–1962)
“No being exists or can exist which is not related to space in some way. God is everywhere, created minds are somewhere, and body is in the space that it occupies; and whatever is neither everywhere nor anywhere does not exist. And hence it follows that space is an effect arising from the first existence of being, because when any being is postulated, space is postulated.”
—Isaac Newton (1642–1727)