Field Electron Emission - Total-energy Distribution

Total-energy Distribution

The energy distribution of the emitted electrons is important both for scientific experiments that use the emitted electron energy distribution to probe aspects of the emitter surface physics and for the field emission sources used in electron beam instruments such as electron microscopes. In the latter case, the "width" (in energy) of the distribution influences how finely the beam can be focused.

The theoretical explanation here follows the approach of Forbes. If ε denotes the total electron energy relative to the emitter Fermi level, and K_p denotes the kinetic energy of the electron parallel to the emitter surface, then the electron's normal energy ε_n (sometimes called its "forwards energy") is defined by

.

Two types of theoretical energy distribution are recognized: the normal-energy distribution (NED), which shows how the energy ε_n is distributed immediately after emission (i.e., immediately outside the tunneling barrier); and the total-energy distribution, which shows how the total energy ε is distributed. When the emitter Fermi level is used as the reference zero level, both ε and ε_n can be either positive or negative.

Energy analysis experiments have been made on field emitters since the 1930s. However, only in the late 1950s was it realized (by Young and Mueller) that these experiments always measured the total energy distribution, which is now usually denoted by j(ε). This is also true (or nearly true) when the emission comes from a small field enhancing protrusion on an otherwise flat surface.

To see how the total energy distribution can be calculated within the framework of a Sommerfeld free-electron-type model, look at the P-T energy-space diagram (P-T="parallel-total").

• Fig. 1. P-T energy-space diagram, showing the region in P-T energy space where traveling-wave electron states exist.

This shows the "parallel kinetic energy" K_p on the horizontal axis and the total energy ε on the vertical axis. An electron inside the bulk metal usually has values of K_p and ε that lie within the lightly shaded area. It can be shown that each element dεdK_p of this energy space makes a contribution to the electron current density incident on the inside of the emitter boundary. Here, z_S is the universal constant (called here the Sommerfeld supply density):

and is the Fermi-Dirac distribution function:

where T is thermodynamic temperature and k_B is Boltzmann's constant.

This element of incident current density sees a barrier of height h given by:

The corresponding escape probability is D(h,F): this may be expanded (approximately) in the form

where D_F is the escape probability for a barrier of unreduced height equal to the local work-function φ. Hence, the element dεdK_p makes a contribution to the emission current density, and the total contribution made by incident electrons with energies in the elementary range dε is thus

,

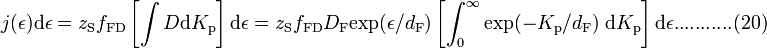where the integral is in principle taken along the strip shown in the diagram, but can in practice be extended to ∞ when the decay-width d_F is very much less than the Fermi energy K_F (which is always the case for a metal). The outcome of the integration can be written:

where and are values appropriate to a barrier of unreduced height h equal to the local work function φ, and is defined by this equation.

For a given emitter, with a given field applied to it, is independent of F, so eq. (21) shows that the shape of the distribution (as ε increases from a negative value well below the Fermi level) is a rising exponential, multiplied by the FD distribution function. This generates the familiar distribution shape first predicted by Young. At low temperatures, goes sharply from 1 to 0 in the vicinity of the Fermi level, and the FWHM of the distribution is given by:

The fact that experimental CFE total energy distributions have this basic shape is a good experimental confirmation that electrons in metals obey Fermi-Dirac statistics.