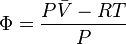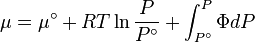Fugacity - Evaluation of Fugacity For A Real Gas

Evaluation of Fugacity For A Real Gas

Fugacity is used to better approximate the chemical potential of real gases than estimations made using the ideal gas law. Yet fugacity allows the use of many of the relationships developed for an idealized system.

In the real world, gases approach ideal gas behavior at low pressures and high temperatures; under such conditions the value of fugacity approaches the value of pressure. Yet no substance is truly ideal. At moderate pressures real gases have attractive interactions and at high pressures intermolecular repulsions become important. Both interactions result in a deviation from "ideal" behavior for which interactions between gas atoms or molecules are ignored.

For a given temperature, the fugacity satisfies the following differential relation:

where is the Gibbs free energy, is the gas constant, is the fluid's molar volume, and is a reference fugacity which is generally taken as 1 bar. For an ideal gas, when, this equation reduces to the ideal gas law.

Thus, for any two physical states at the same temperature, represented by subscripts 1 and 2, the ratio of the two fugacities is as follows:

For an ideal gas, this becomes simply or

But for, every gas is an ideal gas. Therefore, fugacity must obey the limit equation

\mathop {\lim }_{P \to 0} \frac{f} {P} = 1

We determine by defining a function

\Phi = \frac{{P\bar V - RT}} {P}

We can obtain values for experimentally easily by measuring, and .

From the expression above we have

\bar V = \frac{{RT}} {P} + \Phi

We can then write

\int_{\mu ^\circ }^\mu {d\mu } = \int_{P^\circ }^P {\bar VdP} = \int_{P^\circ }^P {\frac{{RT}} {P}dP} + \int_{P^\circ }^P {\Phi dP}

Where

\mu = \mu ^\circ + RT\ln \frac{P} {{P^\circ }} + \int_{P^\circ }^P {\Phi dP}

Since the expression for an ideal gas was chosen to be \mu = \mu ^\circ + RT\ln \frac{f} {{f^\circ }},we must have

\mu ^\circ + RT\ln \frac{f} {{f^\circ }} = \mu ^\circ + RT\ln \frac{P} {{P^\circ }} + \int_{P^\circ }^P {\Phi dP}
\Rightarrow RT\ln \frac{f} {{f^\circ }} - RT\ln \frac{P} {{P^\circ }} = \int_{P^\circ }^P {\Phi dP}
RT\ln \frac{{fP^\circ }} {{Pf^\circ }} = \int_{P^\circ }^P {\Phi dP}

Suppose we choose . Since, we obtain

RT\ln \frac{f} {P} = \int_0^P {\Phi dP}

The fugacity coefficient is defined as = f/P (note that for an ideal gas, = 1.0), and it will then verify

\ln \phi = \frac{1} {{RT}}\int_0^P {\Phi dP}

The integral can be evaluated via graphical integration if we experimentally measure values for while varying .

We can then find the fugacity coefficient of a gas at a given pressure and calculate

The reference state for the expression of a real gas’ chemical potential is taken to be “ideal gas, at = 1 bar and temperature ”. Since in the reference state the gas is considered to be ideal (it is an hypothetical reference state), we can write that for the real gas

\mu = \mu ^\circ + RT\ln \frac{f} {{P^\circ }}

Read more about this topic:  Fugacity

Famous quotes containing the words evaluation of, evaluation, real and/or gas:

    “Good critical writing is measured by the perception and evaluation of the subject; bad critical writing by the necessity of maintaining the professional standing of the critic.”
    —Raymond Chandler (1888–1959)

    “Evaluation is creation: hear it, you creators! Evaluating is itself the most valuable treasure of all that we value. It is only through evaluation that value exists: and without evaluation the nut of existence would be hollow. Hear it, you creators!”
    —Friedrich Nietzsche (1844–1900)

    “...one of my motivating forces has been to recreate the world I know into a world I wish I could be in. Hence my optimism and happy endings. But I’ve never dreamed I could actually reshape the real world.”
    —Kristin Hunter (b. 1931)

    “A new father quickly learns that his child invariably comes to the bathroom at precisely the times when he’s in there, as if he needed company. The only way for this father to be certain of bathroom privacy is to shave at the gas station.”
    —Bill Cosby (20th century)