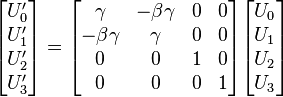Minkowski Space - Lorentz Transformations and Symmetry

Lorentz Transformations and Symmetry

The Poincaré group is the group of all isometries of Minkowski spacetime including boosts, rotations, and translations. The Lorentz group is the subgroup of isometries which leave the origin fixed and includes the boosts and rotations; members of this subgroup are called Lorentz transformations. Among the simplest Lorentz transformations is a Lorentz boost. The archetypal Lorentz boost is

\begin{bmatrix} U'_0 \\ U'_1 \\ U'_2 \\ U'_3 \end{bmatrix} = \begin{bmatrix} \gamma&-\beta \gamma&0&0\\ -\beta \gamma&\gamma&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix} \begin{bmatrix} U_0 \\ U_1 \\ U_2 \\ U_3 \end{bmatrix}\

where

is the Lorentz factor, and

All four-vectors in Minkowski space transform according to the same formula under Lorentz transformations. Minkowski diagrams illustrate Lorentz transformations.

Read more about this topic:  Minkowski Space

Famous quotes containing the word symmetry:

    “What makes a regiment of soldiers a more noble object of view than the same mass of mob? Their arms, their dresses, their banners, and the art and artificial symmetry of their position and movements.”
    —George Gordon Noel Byron (1788–1824)