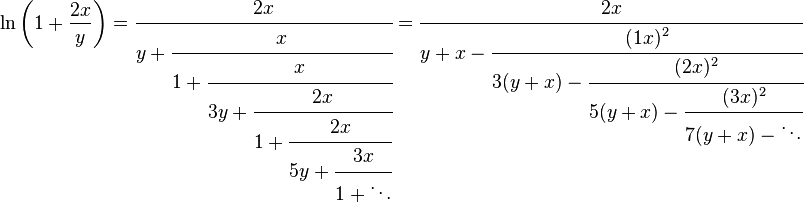Natural Logarithm - Continued Fractions

Continued Fractions

While no simple continued fractions are available, several generalized continued fractions are, including:

\ln (1+x)=\frac{x^1}{1}-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\frac{x^5}{5}-\cdots= \cfrac{x}{1-0x+\cfrac{1^2x}{2-1x+\cfrac{2^2x}{3-2x+\cfrac{3^2x}{4-3x+\cfrac{4^2x}{5-4x+\ddots}}}}}
\ln \left( 1+\frac{2x}{y} \right) = \cfrac{2x} {y+\cfrac{x} {1+\cfrac{x} {3y+\cfrac{2x} {1+\cfrac{2x} {5y+\cfrac{3x} {1+\ddots}}}}}} = \cfrac{2x} {y+x-\cfrac{(1x)^2} {3(y+x)-\cfrac{(2x)^2} {5(y+x)-\cfrac{(3x)^2} {7(y+x)-\ddots}}}}

Read more about this topic:  Natural Logarithm

Famous quotes containing the word continued:

    “There is not any present moment that is unconnected with some future one. The life of every man is a continued chain of incidents, each link of which hangs upon the former. The transition from cause to effect, from event to event, is often carried on by secret steps, which our foresight cannot divine, and our sagacity is unable to trace. Evil may at some future period bring forth good; and good may bring forth evil, both equally unexpected.”
    —Joseph Addison (1672–1719)