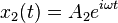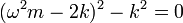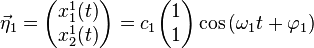Normal Mode - Coupled Oscillators

Coupled Oscillators

Consider two equal bodies (not affected by gravity), each of mass, m, attached to three springs, each with spring constant, k. They are attached in the following manner:

where the edge points are fixed and cannot move. We'll use x1(t) to denote the horizontal displacement of the left mass, and x2(t) to denote the displacement of the right mass.

If we denote acceleration (the second derivative of x(t) with respect to time) as, the equations of motion are:

m \ddot x_1 = - k x_1 + k (x_2 - x_1) = - 2 k x_1 + k x_2 \,\!
m \ddot x_2 = - k x_2 + k (x_1 - x_2) = - 2 k x_2 + k x_1 \,\!

Since we expect oscillatory motion, we try:

x_1(t) = A_1 e^{i \omega t} \,\!
x_2(t) = A_2 e^{i \omega t} \,\!

Substituting these into the equations of motion gives us:

-\omega^2 m A_1 e^{i \omega t} = - 2 k A_1 e^{i \omega t} + k A_2 e^{i \omega t} \,\!
-\omega^2 m A_2 e^{i \omega t} = k A_1 e^{i \omega t} - 2 k A_2 e^{i \omega t} \,\!

Since the exponential factor is common to all terms, we omit it and simplify:

(\omega^2 m - 2 k) A_1 + k A_2 = 0 \,\!
k A_1 + (\omega^2 m - 2 k) A_2 = 0 \,\!

And in matrix representation:

\begin{bmatrix} \omega^2 m - 2 k & k \\ k & \omega^2 m - 2 k \end{bmatrix} \begin{pmatrix} A_1 \\ A_2 \end{pmatrix} = 0

For this equation to have a non-trivial solution, the matrix on the left must be singular i.e. must not be invertible, such that one cannot multiply both sides of the equation by the inverse, leaving the right matrix equal to zero. It follows that the determinant of the matrix must be equal to 0, so:

(\omega^2 m - 2 k)^2 - k^2 = 0 \,\!

Solving for, we have two solutions:

If we substitute ω1 into the matrix and solve for (A1, A2), we get (1, 1). If we substitute ω2, we get (1, −1). (These vectors are eigenvectors, and the frequencies are eigenvalues.)

The first normal mode is:

\vec \eta_1 = \begin{pmatrix} x^1_1(t) \\ x^1_2(t) \end{pmatrix} = c_1 \begin{pmatrix} 1 \\ 1 \end{pmatrix} \cos{(\omega_1 t + \varphi_1)}

Which corresponds to both masses moving in the same direction at the same time.

The second normal mode is:

\vec \eta_2 = \begin{pmatrix} x^2_1(t) \\ x^2_2(t) \end{pmatrix} = c_2 \begin{pmatrix} 1 \\ -1 \end{pmatrix} \cos{(\omega_2 t + \varphi_2)}

This corresponds to the masses moving in the opposite directions, while the center of mass remains stationary.

The general solution is a superposition of the normal modes where c1, c2, φ1, and φ2, are determined by the initial conditions of the problem.

The process demonstrated here can be generalized and formulated using the formalism of Lagrangian mechanics or Hamiltonian mechanics.

Read more about this topic:  Normal Mode

Famous quotes containing the word coupled:

    “Legislators or revolutionaries who promise equality coupled with freedom are either phantasts or charlatans.”
    —Johann Wolfgang Von Goethe (1749–1832)