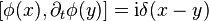Quantum Field Theory
The path integral formulation was very important for the development of quantum field theory. Both the Schrödinger and Heisenberg approaches to quantum mechanics single out time, and are not in the spirit of relativity. For example, the Heisenberg approach requires that scalar field operators obey the commutation relation
for x and y two simultaneous spatial positions, and this is not a relativistically invariant concept. The results of a calculation are covariant at the end of the day, but the symmetry is not apparent in intermediate stages. If naive field theory calculations did not produce infinite answers in the continuum limit, this would not have been such a big problem – it would just have been a bad choice of coordinates. But the lack of symmetry means that the infinite quantities must be cut off, and the bad coordinates make it nearly impossible to cut off the theory without spoiling the symmetry. This makes it difficult to extract the physical predictions, which require a careful limiting procedure.
The problem of lost symmetry also appears in classical mechanics, where the Hamiltonian formulation also superficially singles out time. The Lagrangian formulation makes the relativistic invariance apparent. In the same way, the path integral is manifestly relativistic. It reproduces the Schrödinger equation, the Heisenberg equations of motion, and the canonical commutation relations and shows that they are compatible with relativity. It extends the Heisenberg type operator algebra to operator product rules which are new relations difficult to see in the old formalism.
Further, different choices of canonical variables lead to very different seeming formulations of the same theory. The transformations between the variables can be very complicated, but the path integral makes them into reasonably straightforward changes of integration variables. For these reasons, the Feynman path integral has made earlier formalisms largely obsolete.
The price of a path integral representation is that the unitarity of a theory is no longer self-evident, but it can be proven by changing variables to some canonical representation. The path integral itself also deals with larger mathematical spaces than is usual, which requires more careful mathematics not all of which has been fully worked out. The path integral historically was not immediately accepted, partly because it took many years to incorporate fermions properly. This required physicists to invent an entirely new mathematical object – the Grassmann variable – which also allowed changes of variables to be done naturally, as well as allowing constrained quantization.
The integration variables in the path integral are subtly non-commuting. The value of the product of two field operators at what looks like the same point depends on how the two points are ordered in space and time. This makes some naive identities fail.
Read more about this topic: Path Integral Formulation
Famous quotes containing the words quantum, field and/or theory:
“A personality is an indefinite quantum of traits which is subject to constant flux, change, and growth from the birth of the individual in the world to his death. A character, on the other hand, is a fixed and definite quantum of traits which, though it may be interpreted with slight differences from age to age and actor to actor, is nevertheless in its essentials forever fixed.”
—Hubert C. Heffner (1901–1985)
“Mine was, as it were, the connecting link between wild and cultivated fields; as some states are civilized, and others half-civilized, and others savage or barbarous, so my field was, though not in a bad sense, a half-cultivated field. They were beans cheerfully returning to their wild and primitive state that I cultivated, and my hoe played the Ranz des Vaches for them.”
—Henry David Thoreau (1817–1862)
“The human species, according to the best theory I can form of it, is composed of two distinct races, the men who borrow and the men who lend.”
—Charles Lamb (1775–1834)