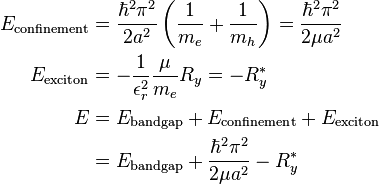Quantum Confinement in Semiconductors
In a semiconductor crystal lattice, the electrons are squeezed together, since no two nearby electrons can share exactly the same energy level according to Pauli exclusion principle, leading to quantum confinement. The energy level can then be modeled using particle in a box, which leads to the conclusion that the energy levels of the quantum dot are dependent on its size. When the size of the quantum dot is smaller than the critical characteristic length called the Exciton Bohr radius, the electrons crowding lead to the splitting of the original energy levels into smaller ones with smaller gaps between each successive level. The Exciton Bohr radius is larger than the Bohr radius due to the effect of dielectric screening and the influence of periodic lattice structure of the crystal. The quantum dots that have radii larger than the Exciton Bohr radius are said to be in the 'weak confinement regime' and the ones that have radii smaller than the Exciton Bohr radius are said to be in the 'strong confinement regime'. Thus, if the size of the quantum dot is small enough that the quantum confinement effects dominate(typically less than 10 nm), the electronic and optical properties change, and the fluorescent wavelength is determined by the size.
The fluorescence of the quantum dots is a result of exciting the valence electron with a certain energy(or wavelength) and the emission of lower energy in the form of photons as the excited electron return to the ground state combining with the hole. The energy of the emitted photon is determined by the size of the quantum dot due to quantum confinement effects. In a simplified model of the excitation, the energy of the emitted photon can be seen as a sum of the band gap energy between occupied level and unoccupied energy level, the confinement energies of the hole and the excited electron, and the bound energy of the exciton(the electron-hole pair):
- Band gap energy
- The band gap can become smaller in the strong confinement regime where the size of the quantum dot is smaller than the Exciton Bohr radius (ab* in the figure) as the energy levels split up. This results in the increase in the total emission energy(the sum of the energy levels in the smaller band gaps in the strong confinement regime is larger than the energy levels in the band gaps of the original levels in the weak confinement regime) and the emission at various wavelengths; which is precisely what happens in the sun, where the quantum confinement effects are completely dominant and the energy levels split up to the degree that the energy spectrum is almost continuous, thus emitting white light.
- Confinement energy
- The exciton entity can be modeled using the particle in the box. The electron and the hole can be seen as hydrogen in the Bohr model with the hydrogen nucleus replaced by the hole of positive charge and negative electron mass. Then the energy levels of the exciton can be represented as the solution to the particle in a box at the ground level (n = 1) with the mass replaced by the reduced mass. Thus by varying the size of the quantum dot, the confinement energy of the exciton can be controlled.
- Bound exciton energy
- There is Coulomb attraction between the negatively charged electron and the positively charged hole. The negative energy involved in the attraction is proportional to Rydberg’s energy and inversely proportional to square of the size-dependent dielectric constant of the semiconductor. When the size of the semiconductor crystal is smaller than the Exciton Bohr radius, the Coulomb interaction must be modified to fit the situation.
Therefore, the sum of these energies can be represented as:
where:
- μ is the reduced mass
- a is the radius
- me is the free electron mass
- mh is the hole mass
- εr is the size-dependent dielectric constant
Although the above equations were derived using simplifying assumptions, the implications are clear; the energy of the quantum dots are dependent on their size due to the quantum confinement effects, which dominate below the critical size leading to changes in the optical properties. This effect of quantum confinement on the quantum dots have been experimentally verified and is a key feature of many emerging electronic structures.
Besides confinement in all three dimensions (i.e., a quantum dot), other quantum confined semiconductors include:
- Quantum wires, which confine electrons or holes in two spatial dimensions and allow free propagation in the third.
- Quantum wells, which confine electrons or holes in one dimension and allow free propagation in two dimensions.
Read more about this topic: Quantum Dot
Famous quotes containing the words quantum and/or confinement:
“But how is one to make a scientist understand that there is something unalterably deranged about differential calculus, quantum theory, or the obscene and so inanely liturgical ordeals of the precession of the equinoxes.”
—Antonin Artaud (1896–1948)
“We’re all of us sentenced to solitary confinement inside our own skins, for life!”
—Tennessee Williams (1914–1983)