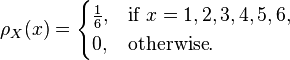Random Variable - Examples

Examples

In a poll an adult person is chosen at random from the British population . The random variable A is the age of the chosen person, and the random variable C the number of children:

The possible outcomes for one coin toss can be described by the sample space = {heads, tails}. We can introduce a real-valued random variable Y that models a $1 payoff for a successful bet on heads as follows:

Y(\omega) = \begin{cases} 1, & \text{if} \ \ \omega = \text{heads} ,\\ 0, & \text{if} \ \ \omega = \text{tails} . \end{cases}

If the coin is equally likely to land on either side then it has a probability mass function given by:

\rho_Y(y) = \begin{cases}\frac{1}{2},& \text{if }y=1,\\ \frac{1}{2},& \text{if }y=0.\end{cases}

A random variable can also be used to describe the process of rolling a die and the possible outcomes. The most obvious representation is to take the set = {1, 2, 3, 4, 5, 6} as the sample space, defining the random variable X to be equal to the number rolled. In this case,

and

\rho_X(x) = \begin{cases}\frac{1}{6},& \text{if }x=1,2,3,4,5,6,\\ 0,& \text{otherwise} .\end{cases}

An example of a continuous random variable would be one based on a spinner that can choose a horizontal direction. Then the values taken by the random variable are directions. We could represent these directions by North, West, East, South, Southeast, etc. However, it is commonly more convenient to map the sample space to a random variable which takes values which are real numbers. This can be done, for example, by mapping a direction to a bearing in degrees clockwise from North. The random variable then takes values which are real numbers from the interval is ½. Instead of speaking of a probability mass function, we say that the probability density of X is 1/360. The probability of a subset of [0, 360) can be calculated by multiplying the measure of the set by 1/360. In general, the probability of a set for a given continuous random variable can be calculated by integrating the density over the given set.

An example of a random variable of mixed type would be based on an experiment where a coin is flipped and the spinner is spun only if the result of the coin toss is heads. If the result is tails, X = −1; otherwise X = the value of the spinner as in the preceding example. There is a probability of ½ that this random variable will have the value −1. Other ranges of values would have half the probability of the last example.

Read more about this topic:  Random Variable

Famous quotes containing the word examples:

    “Histories are more full of examples of the fidelity of dogs than of friends.”
    —Alexander Pope (1688–1744)

    “It is hardly to be believed how spiritual reflections when mixed with a little physics can hold people’s attention and give them a livelier idea of God than do the often ill-applied examples of his wrath.”
    —G.C. (Georg Christoph)

    “No rules exist, and examples are simply life-savers answering the appeals of rules making vain attempts to exist.”
    —André Breton (1896–1966)