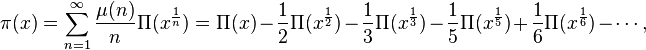History
"…es ist sehr wahrscheinlich, dass alle Wurzeln reell sind. Hiervon wäre allerdings ein strenger Beweis zu wünschen; ich habe indess die Aufsuchung desselben nach einigen flüchtigen vergeblichen Versuchen vorläufig bei Seite gelassen, da er für den nächsten Zweck meiner Untersuchung entbehrlich schien."
"…it is very probable that all roots are real. Of course one would wish for a rigorous proof here; I have for the time being, after some fleeting vain attempts, provisionally put aside the search for this, as it appears dispensable for the next objective of my investigation."
In his 1859 paper On the Number of Primes Less Than a Given Magnitude Riemann found an explicit formula for the number of primes π(x) less than a given number x. His formula was given in terms of the related function
which counts primes where a prime power pn counts as 1/n of a prime. The number of primes can be recovered from this function by
where μ is the Möbius function. Riemann's formula is then
where the sum is over the nontrivial zeros of the zeta function and where Π0 is a slightly modified version of Π that replaces its value at its points of discontinuity by the average of its upper and lower limits:
The summation in Riemann's formula is not absolutely convergent, but may be evaluated by taking the zeros ρ in order of the absolute value of their imaginary part. The function Li occurring in the first term is the (unoffset) logarithmic integral function given by the Cauchy principal value of the divergent integral
The terms Li(xρ) involving the zeros of the zeta function need some care in their definition as Li has branch points at 0 and 1, and are defined (for x > 1) by analytic continuation in the complex variable ρ in the region Re(ρ) > 0, i.e. they should be considered as Ei(ρ ln x). The other terms also correspond to zeros: the dominant term Li(x) comes from the pole at s = 1, considered as a zero of multiplicity −1, and the remaining small terms come from the trivial zeros. For some graphs of the sums of the first few terms of this series see Riesel & Göhl (1970) or Zagier (1977).
This formula says that the zeros of the Riemann zeta function control the oscillations of primes around their "expected" positions. Riemann knew that the non-trivial zeros of the zeta function were symmetrically distributed about the line s = 1/2 + it, and he knew that all of its non-trivial zeros must lie in the range 0 ≤ Re(s) ≤ 1. He checked that a few of the zeros lay on the critical line with real part 1/2 and suggested that they all do; this is the Riemann hypothesis.
Read more about this topic: Riemann Hypothesis
Famous quotes containing the word history:
“History does nothing; it does not possess immense riches, it does not fight battles. It is men, real, living, who do all this.... It is not “history” which uses men as a means of achieving—as if it were an individual person—its own ends. History is nothing but the activity of men in pursuit of their ends.”
—Karl Marx (1818–1883)
“The history of the genesis or the old mythology repeats itself in the experience of every child. He too is a demon or god thrown into a particular chaos, where he strives ever to lead things from disorder into order.”
—Ralph Waldo Emerson (1803–1882)
“It is remarkable how closely the history of the apple tree is connected with that of man.”
—Henry David Thoreau (1817–1862)