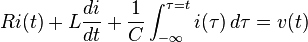RLC Circuit - Series RLC Circuit

Series RLC Circuit

Figure 1. RLC series circuit
V - the voltage of the power source
I - the current in the circuit
R - the resistance of the resistor
L - the inductance of the inductor
C - the capacitance of the capacitor

In this circuit, the three components are all in series with the voltage source. The governing differential equation can be found by substituting into Kirchhoff's voltage law (KVL) the constitutive equation for each of the three elements. From KVL,

v_R+v_L+v_C=v(t) \,

where are the voltages across R, L and C respectively and is the time varying voltage from the source. Substituting in the constitutive equations,

Ri(t) + L { {di} \over {dt}} + {1 \over C} \int_{-\infty}^{\tau=t} i(\tau)\, d\tau = v(t)

For the case where the source is an unchanging voltage, differentiating and dividing by L leads to the second order differential equation:

{{d^2 i(t)} \over {dt^2}} +{R \over L} {{di(t)} \over {dt}} + {1 \over {LC}} i(t) = 0

This can usefully be expressed in a more generally applicable form:

{{d^2 i(t)} \over {dt^2}} + 2 \alpha {{di(t)} \over {dt}} + {\omega_0}^2 i(t) = 0

and are both in units of angular frequency. is called the neper frequency, or attenuation, and is a measure of how fast the transient response of the circuit will die away after the stimulus has been removed. Neper occurs in the name because the units can also be considered to be nepers per second, neper being a unit of attenuation. is the angular resonance frequency.

For the case of the series RLC circuit these two parameters are given by:

and

A useful parameter is the damping factor, which is defined as the ratio of these two,

In the case of the series RLC circuit, the damping factor is given by,

The value of the damping factor determines the type of transient that the circuit will exhibit. Some authors do not use and call the damping factor.

Read more about this topic:  RLC Circuit

Famous quotes containing the words series and/or circuit:

    “History is nothing but a procession of false Absolutes, a series of temples raised to pretexts, a degradation of the mind before the Improbable.”
    —E.M. Cioran (b. 1911)

    “each new victim treads unfalteringly
    The never altered circuit of his fate,
    Bringing twelve peers as witness
    Both to his starry rise and starry fall.”
    —Robert Graves (1895–1985)