Scattering - Electromagnetic Scattering

Electromagnetic Scattering

Electromagnetic waves are one of the best known and most commonly encountered forms of radiation that undergo scattering. Scattering of light and radio waves (especially in radar) is particularly important. Several different aspects of electromagnetic scattering are distinct enough to have conventional names. Major forms of elastic light scattering (involving negligible energy transfer) are Rayleigh scattering and Mie scattering. Inelastic scattering includes Brillouin scattering, Raman scattering, inelastic X-ray scattering and Compton scattering.

Light scattering is one of the two major physical processes that contribute to the visible appearance of most objects, the other being absorption. Surfaces described as white owe their appearance to multiple scattering of light by internal or surface inhomogeneities in the object, for example by the boundaries of transparent microscopic crystals that make up a stone or by the microscopic fibers in a sheet of paper. More generally, the gloss (or lustre or sheen) of the surface is determined by scattering. Highly scattering surfaces are described as being dull or having a matte finish, while the absence of surface scattering leads to a glossy appearance, as with polished metal or stone. Spectral absorption, the selective absorption of certain colors, determines the color of most objects with some modification by elastic scattering. The apparent blue color of veins in skin is a common example where both spectral absorption and scattering play important and complex roles in the coloration. Light scattering can also create color without absorption, often shades of blue, as with the sky (Rayleigh scattering), the human blue iris, and the feathers of some birds (Prum et al. 1998). However, resonant light scattering in nanoparticles can produce many different highly saturated and vibrant hues, especially when surface plasmon resonance is involved (Roqué et al. 2006).

Models of light scattering can be divided into three domains based on a dimensionless size parameter, α which is defined as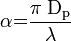

where πD_p is the circumference of a particle and λ is the wavelength of incident radiation. Based on the value of α, these domains are:

: Rayleigh scattering (small particle compared to wavelength of light)

: Mie scattering (particle about the same size as wavelength of light)

: Geometric scattering (particle much larger than wavelength of light)

Rayleigh scattering is a process in which electromagnetic radiation (including light) is scattered by a small spherical volume of variant refractive index, such as a particle, bubble, droplet, or even a density fluctuation. This effect was first modeled successfully by Lord Rayleigh, from whom it gets its name. In order for Rayleigh's model to apply, the sphere must be much smaller in diameter than the wavelength (λ) of the scattered wave; typically the upper limit is taken to be about 1/10 the wavelength. In this size regime, the exact shape of the scattering center is usually not very significant and can often be treated as a sphere of equivalent volume. The inherent scattering that radiation undergoes passing through a pure gas is due to microscopic density fluctuations as the gas molecules move around, which are normally small enough in scale for Rayleigh's model to apply. This scattering mechanism is the primary cause of the blue color of the Earth's sky on a clear day, as the shorter blue wavelengths of sunlight passing overhead are more strongly scattered than the longer red wavelengths according to Rayleigh's famous 1/λ4 relation. Along with absorption, such scattering is a major cause of the attenuation of radiation by the atmosphere. The degree of scattering varies as a function of the ratio of the particle diameter to the wavelength of the radiation, along with many other factors including polarization, angle, and coherence.

For larger diameters, the problem of electromagnetic scattering by spheres was first solved by Gustav Mie, and scattering by spheres larger than the Rayleigh range is therefore usually known as Mie scattering. In the Mie regime, the shape of the scattering center becomes much more significant and the theory only applies well to spheres and, with some modification, spheroids and ellipsoids. Closed-form solutions for scattering by certain other simple shapes exist, but no general closed-form solution is known for arbitrary shapes.

Both Mie and Rayleigh scattering are considered elastic scattering processes, in which the energy (and thus wavelength and frequency) of the light is not substantially changed. However, electromagnetic radiation scattered by moving scattering centers does undergo a Doppler shift, which can be detected and used to measure the velocity of the scattering center/s in forms of techniques such as LIDAR and radar. This shift involves a slight change in energy.

At values of the ratio of particle diameter to wavelength more than about 10, the laws of geometric optics are mostly sufficient to describe the interaction of light with the particle, and at this point the interaction is not usually described as scattering.

For modeling of scattering in cases where the Rayleigh and Mie models do not apply such as irregularly shaped particles, there are many numerical methods that can be used. The most common are finite-element methods which solve Maxwell's equations to find the distribution of the scattered electromagnetic field. Sophisticated software packages exist which allow the user to specify the refractive index or indices of the scattering feature in space, creating a 2- or sometimes 3-dimensional model of the structure. For relatively large and complex structures, these models usually require substantial execution times on a computer.