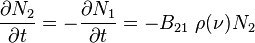Mathematical Model
Stimulated emission can be modelled mathematically by considering an atom that may be in one of two electronic energy states, a lower level state (possibly the ground state) (1) and an excited state (2), with energies E1 and E2 respectively.
If the atom is in the excited state, it may decay into the lower state by the process of spontaneous emission, releasing the difference in energies between the two states as a photon. The photon will have frequency ν and energy hν, given by:
where h is Planck's constant.
Alternatively, if the excited-state atom is perturbed by an electric field of frequency, it may emit an additional photon of the same frequency and in phase, thus augmenting the external field, leaving the atom in the lower energy state. This process is known as stimulated emission.
In a group of such atoms, if the number of atoms in the excited state is given by N2, the rate at which stimulated emission occurs is given by:
where the proportionality constant B21 is known as the Einstein B coefficient for that particular transition, and ρ(ν) is the radiation density of the incident field at frequency ν. The rate of emission is thus proportional to the number of atoms in the excited state N2, and to the density of incident photons.
At the same time, there will be a process of atomic absorption which removes energy from the field while raising electrons from the lower state to the upper state. Its rate is given by an essentially identical equation:
 .
.
The rate of absorption is thus proportional to the number of atoms in the lower state, N1. Einstein showed that the coefficient for this transition must be identical to that for stimulated emission:
- .
Thus absorption and stimulated emission are reverse processes proceeding at somewhat different rates. Another way of viewing this is to look at the net stimulated emission or absorption viewing it as a single process. The net rate of transitions from E2 to E1 due to this combined process can be found by adding their respective rates, given above:
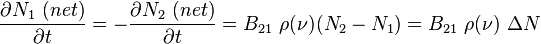 .
.
Thus a net power is released into the electric field equal to the photon energy hν times this net transition rate. In order for this to be a positive number, indicating net stimulated emission, there must be more atoms in the excited state than in the lower level: . Otherwise there is net absorption and the power of the wave is reduced during passage through the medium. The special condition is known as a population inversion, a rather unusual condition that must be effected in the gain medium of a laser.
The notable characteristic of stimulated emission compared to everyday light sources (which depend on spontaneous emission) is that the emitted photons have the same frequency, phase, polarization, and direction of propagation as the incident photons. The photons involved are thus mutually coherent. When a population inversion is present, therefore, optical amplification of incident radiation will take place.
Although energy generated by stimulated emission is always at the exact frequency of the field which has stimulated it, the above rate equation refers only to excitation at the particular optical frequency corresponding to the energy of the transition. At frequencies offset from the strength of stimulated (or spontaneous) emission will be decreased according to the so-called "line shape". Considering only homogeneous broadening affecting an atomic or molecular resonance, the spectral line shape function is described as a Lorentzian distribution:
where is the full width at half maximum or FWHM bandwidth.
The peak value of the Lorentzian line shape occurs at the line center, . A line shape function can be normalized so that its value at is unity; in the case of a Lorentzian we obtain:
- .
Thus stimulated emission at frequencies away from is reduced by this factor. In practice there may also be broadening of the line shape due to inhomogeneous broadening, most notably due to the Doppler effect resulting from the distribution of velocities in a gas at a certain temperature. This has a Gaussian shape and reduces the peak strength of the line shape function. In a practical problem the full line shape function can be computed through a convolution of the individual line shape functions involved. Therefore optical amplification will add power to an incident optical field at frequency at a rate given by:
- .
Read more about this topic: Stimulated Emission
Famous quotes containing the words mathematical and/or model:
“It is by a mathematical point only that we are wise, as the sailor or the fugitive slave keeps the polestar in his eye; but that is sufficient guidance for all our life. We may not arrive at our port within a calculable period, but we would preserve the true course.”
—Henry David Thoreau (1817–1862)
“Socrates, who was a perfect model in all great qualities, ... hit on a body and face so ugly and so incongruous with the beauty of his soul, he who was so madly in love with beauty.”
—Michel de Montaigne (1533–1592)