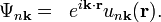Origin of Surface States At Condensed Matter Interfaces
As stated by Bloch's theorem, eigenstates of the single-electron Schrödinger equation with a perfectly periodic potential, a crystal, are Bloch waves
Here is a function with the same periodicity as the crystal, n is the band index and k is the wave number. The allowed wave numbers for a given potential are found by applying the usual Born–von Karman cyclic boundary conditions . The termination of a crystal, i.e. the formation of a surface, obviously causes deviation from perfect periodicity. Consequently, if the cyclic boundary conditions are abandoned in the direction normal to the surface the behavior of electrons will deviate from the behavior in the bulk and some modifications of the electronic structure has to be expected.
A simplified model of the crystal potential in one dimension can be sketched as shown in figure 1 . In the crystal, the potential has the periodicity, a, of the lattice while close to the surface it has to somehow attain the value of the vacuum level. The step potential (solid line) shown in figure 1 is an oversimplification which is mostly convenient for simple model calculations. At a real surface the potential is influenced by image charges and the formation of surface dipoles and it rather looks as indicated by the dashed line.
Given the potential in figure 1, it can be shown that the one-dimensional single-electron Schrödinger equation gives two qualitatively different types of solutions.
- The first type of states (see figure 2) extends into the crystal and has Bloch character there. These type of solutions correspond to bulk states which terminate in an exponentially decaying tail reaching into the vacuum.
- The second type of states (see figure 3) decays exponentially both into the vacuum and the bulk crystal. These type of solutions correspond to states, with wave functions localized close to the crystal surface.
The first type of solution can be obtained for both metals and semiconductors. In semiconductors though, the associated eigenenergies have to belong to one of the allowed energy bands. The second type of solution exists in forbidden energy gap of semiconductors as well as in local gaps of the projected band structure of metals. It can be shown that the energies of these states all lie within the band gap. As a consequence, in the crystal these states are characterized by an imaginary wavenumber leading to an exponential decay into the bulk.
Read more about this topic: Surface States
Famous quotes containing the words origin, surface, states, condensed and/or matter:
“Though I do not believe that a plant will spring up where no seed has been, I have great faith in a seed,—a, to me, equally mysterious origin for it.”
—Henry David Thoreau (1817–1862)
“It was a pretty game, played on the smooth surface of the pond, a man against a loon.”
—Henry David Thoreau (1817–1862)
“On the whole, the great success of marriage in the States is due partly to the fact that no American man is ever idle, and partly to the fact that no American wife is considered responsible for the quality of her husband’s dinners.”
—Oscar Wilde (1854–1900)
“If you read only the best, you will have no need of reading the other books, because the latter are nothing but a rehash of the best and the oldest. To read Shakespeare, Plato, Dante, Milton, Spenser, Chaucer, and their compeers in prose, is to read in condensed form what all others have diluted.”
—Anna C. Brackett (1836–1911)
“No matter how much faculty of idle seeing a man has, the step from knowing to doing is rarely taken. ‘Tis a step out of the chalk circle of imbecility into fruitfulness.”
—Ralph Waldo Emerson (1803–1882)