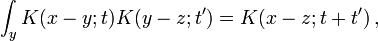Free Propagator
The narrow-width limit of the Gaussian wavepacket solution discussed is the free propagator kernel K. For other differential equations, this is sometimes called the Green's function, but in quantum mechanics it is traditional to reserve the name Green's function for the time Fourier transform of K.
Returning to one dimension for simplicity, when a is the infinitesimal quantity ε, the Gaussian initial condition, rescaled so that its integral is one:
becomes a delta function, δ(x), so that its time evolution,
gives the propagator.
Note that a very narrow initial wavepacket instantly becomes infinitely wide, but with a phase which is more rapidly oscillatory at large values of x. This might seem strange—the solution goes from being localized at one point to being "everywhere" at all later times, but it is a reflection of the enormous momentum uncertainty of a localized particle. Also note that the norm of the wavefunction is infinite, but this is also correct, since the square of a delta function is divergent in the same way.
The factor involving ε is an infinitesimal quantity which is there to make sure that integrals over K are well defined. In the limit that ε→0, K becomes purely oscillatory, and integrals of K are not absolutely convergent. In the remainder of this section, it will be set to zero, but in order for all the integrations over intermediate states to be well defined, the limit ε→0 is to be only taken after the final state is calculated.
The propagator is the amplitude for reaching point x at time t, when starting at the origin, x=0. By translation invariance, the amplitude for reaching a point x when starting at point y is the same function, only now translated,
In the limit when t is small, the propagator, of course, goes to a delta function,
but only in the sense of distributions: The integral of this quantity multiplied by an arbitrary differentiable test function gives the value of the test function at zero. To see this, note that the integral over all space of K equals 1 at all times:
since this integral is the inner-product of K with the uniform wavefunction. But the phase factor in the exponent has a nonzero spatial derivative everywhere except at the origin, and so when the time is small there are fast phase cancellations at all but one point. This is rigorously true when the limit ε→0 is taken at the very end.
So the propagation kernel is the (future) time evolution of a delta function, and it is continuous, in a sense: it goes to the initial delta function at small times. If the initial wavefunction is an infinitely narrow spike at position y,
it becomes the oscillatory wave:
Now, since every function can be written as a weighted sum of such narrow spikes,
the time evolution of every function ψ0 is determined by the propagation kernel K:
Thus, this is a formal way to express the general solution. The interpretation of this expression is that the amplitude for a particle to be found at point x at time t is the amplitude that it started at y, times the amplitude that it went from y to x, summed over all the possible starting points. In other words, it is a convolution of the kernel K with the arbitrary initial condition ψ0,
Since the amplitude to travel from x to y after a time t+t ' can be considered in two steps, the propagator obeys the identity:
which can be interpreted as follows: the amplitude to travel from x to z in time t+t ' is the sum of the amplitude to travel from x to y in time t, multiplied by the amplitude to travel from y to z in time t ', summed over all possible intermediate states y. This is a property of an arbitrary quantum system, and by subdividing the time into many segments, it allows the time evolution to be expressed as a path integral.
Read more about this topic: Wave Packet
Famous quotes containing the word free:
“If there be a love pure and free from the admixture of our other passions, it is that which lies hidden in the bottom of our heart, and which we know not ourselves.”
—François, Duc De La Rochefoucauld (1613–1680)