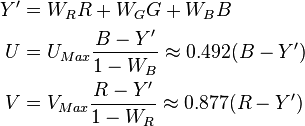YUV - Conversion To/from RGB | Conversion RGB

Conversion To/from RGB

Y'UV signals are typically created from RGB (red, green and blue) source. Weighted values of R, G, and B are summed to produce Y', a measure of overall brightness or luminance. U and V are computed as scaled differences between Y' and the B and R values.

Defining the following constants:

$\begin{align} W_R &= 0.299 \\ W_B &= 0.114 \\ W_G &= 1 - W_R - W_B = 0.587 \\ U_{Max} &= 0.436 \\ V_{Max} &= 0.615 \end{align}$

Y'UV is computed from RGB as follows:

$\begin{align} Y' &= W_R R + W_G G + W_B B \\ U &= U_{Max} \frac{B - Y'}{1 - W_B} \approx 0.492(B - Y') \\ V &= V_{Max} \frac{R - Y'}{1 - W_R} \approx 0.877(R - Y') \end{align}$

The resulting ranges of Y', U, and V respectively are, and .

Inverting the above transformation converts Y'UV to RGB:

$\begin{align} R &= Y' + V \frac{1 - W_R}{V_{Max}} = Y' + \frac{V}{0.877}\\ G &= \frac{Y'}{W_G} - U \frac{W_B (1 - W_B)}{U_{Max} W_G} - V \frac{W_R (1 - W_R)}{V_{Max} W_G} = \frac{Y'}{0.587} - \frac{Y'+ 2.032 U}{0.587} - \frac{Y'+1.140 V}{0.587} = -1.7036 Y'-3.462 U - 1.942 V\\ B &= Y' + U \frac{1 - W_B}{U_{Max}} =Y' + \frac{U}{0.492} \end{align}$

Equivalently, substituting values for the constants and expressing them as matrices gives:

$\begin{bmatrix} Y' \\ U \\ V \end{bmatrix} = \begin{bmatrix} 0.299 & 0.587 & 0.114 \\ -0.14713 & -0.28886 & 0.436 \\ 0.615 & -0.51499 & -0.10001 \end{bmatrix} \begin{bmatrix} R \\ G \\ B \end{bmatrix}$

$\begin{bmatrix} R \\ G \\ B \end{bmatrix} = \begin{bmatrix} 1 & 0 & 1.13983 \\ 1 & -0.39465 & -0.58060 \\ 1 & 2.03211 & 0 \end{bmatrix} \begin{bmatrix} Y' \\ U \\ V \end{bmatrix}$