Zero Divisor - Examples

Examples

  • The ring Z of integers has no zero divisors, but in the ring Z/4Z the number 2 is a zero divisor: 2 × 2 = 4 = 0 as a divisor of 4, which is a composite number.
  • A nonzero nilpotent element is always a zero-divisor (left and right).
  • A nonzero idempotent element is always a two-sided zero divisor, provided that it is not 1.
  • An example of a zero divisor in the ring of 2-by-2 matrices (over any unital ring except trivial) is the matrix
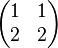
    \begin{pmatrix}1&1\\ 2&2\end{pmatrix}
    because for instance
    \begin{pmatrix}1&1\\ 2&2\end{pmatrix}\begin{pmatrix}1&1\\ -1&-1\end{pmatrix}=\begin{pmatrix}-2&1\\ -2&1\end{pmatrix}\begin{pmatrix}1&1\\ 2&2\end{pmatrix}=\begin{pmatrix}0&0\\ 0&0\end{pmatrix}.
  • Actually, the simplest example of a pair of zero divisor matrices is
    \begin{pmatrix}1&0\\0&0\end{pmatrix} \begin{pmatrix}0&0\\0&1\end{pmatrix} = \begin{pmatrix}0&0\\0&0\end{pmatrix} = \begin{pmatrix}0&0\\0&1\end{pmatrix} \begin{pmatrix}1&0\\0&0\end{pmatrix}.
  • A direct product of two or more non-trivial rings always has zero divisors similarly to the 2 × 2-matrix example just above (the ring of diagonal 2 × 2 matrices over a ring R is the same as the direct product R × R).
  • Here is an example of a ring with an element that is a zero divisor on one side only. Let S be the set of all sequences of integers (a1, a2, a3, …). Take for the ring all additive maps from S to S, with pointwise addition and composition as the ring operations. (That is, our ring is End(S), the endomorphisms of the additive group S.) Three examples of elements of this ring are the right shift R(a1, a2, a3, …) = (0, a1, a2, …), the left shift L(a1, a2, a3, …) = (a2, a3, a4, …), and a third additive map T(a1, a2, a3, …) = (a1, 0, 0, …). All three of these additive maps are not zero, and the composites L T and T R are both zero, so L is a left zero divisor and R is a right zero divisor in the ring of additive maps from S to S. However, L is not a right zero divisor and R is not a left zero divisor: the composite L R is the identity, so if some additive map f from S to S satisfies f L= 0 then composing both sides of this equation on the right with R shows (f L) R = f (L R) = f 1 = f has to be 0, and similarly if some f satisfies R f = 0 then composing both sides on the left with L shows f is 0.

Continuing with this example, note that while R L is a left zero divisor ((R L) T = R (L T) is 0 because L T is), L R is not a zero divisor on either side because it is the identity.

Concretely, we can interpret additive maps from S to S as countably infinite matrices. The matrix

A = \begin{pmatrix} 0 & 1 & 0 &0&0&\\ 0 & 0 & 1 &0&0&\cdots\\ 0 & 0 & 0 &1&0&\\ 0&0&0&0&1&\\ &&\vdots&&&\ddots \end{pmatrix}

realizes L explicitly (just apply the matrix to a vector and see the effect is exactly a left shift) and the transpose B = AT realizes the right shift on S. That A B is the identity matrix is the same as saying L R is the identity. In particular, as matrices A is a left zero divisor but not a right zero divisor.

Read more about this topic:  Zero Divisor

Famous quotes containing the word examples:

    “No rules exist, and examples are simply life-savers answering the appeals of rules making vain attempts to exist.”
    —André Breton (1896–1966)

    “Histories are more full of examples of the fidelity of dogs than of friends.”
    —Alexander Pope (1688–1744)

    “In the examples that I here bring in of what I have [read], heard, done or said, I have refrained from daring to alter even the smallest and most indifferent circumstances. My conscience falsifies not an iota; for my knowledge I cannot answer.”
    —Michel de Montaigne (1533–1592)